Матч 417, Тройной прыжок (TripleJump)

Дивизион 2, Уровень 3

Тройной прыжок совершается следующим образом. Прыгун разгоняется, добегает до определенной отметки и совершает три последовательных прыжка. Победителем является тот, чья суммарная длина прыжков наибольшая.

Вы прыгаете последним. Все Ваши соперники уже совершили прыжки, их результаты заданы в массиве opponents.

Первый свой прыжок Вы уже совершили, его длина равна first. Длина каждого из оставшихся прыжков может с равной вероятностью принимать любое значение из отрезка [lower, upper], и не обязательно быть целым. Вы хотите вычислить вероятность того, что займете i - ое место. Необходимо построить массив длины n + 1 (n равно числу соперников), i -ый элемент которого (индексация массива начинается с 0) содержит вероятность того, что Вы займете (i + 1) - ое место. Место, занятое Вами, равняется единице плюс количество соперников, которые прыгнули дальше Вас.

Класс: TripleJump

Метод: vector<double> getProbabilities(int lower, int upper,

int first, vector<int> opponents)

Ограничения: 1 £ lower £ 1000, lower £ upper £ 1000, lower £ first £ upper, opponents содержит от 1 до 50 элементов, 1 £ opponents[i] £ 3000.

Вход. Целые значения lower, upper , first и массив длин прыжков opponents.

Выход. Массив, содержащий вероятности того, что Вы займете первое, второе, …, последнее место.

Пример входа

lower	upper	first	opponents
1	2	1	{1,2,3,4}
3	7	5	{9,9,19,19,19}
1	10	5	{1,2,3,5,10,11,12,19}

Пример выхода

{0.5, 0.5, 0.0, 0.0, 0.0}

{0.0, 0.0, 0.0, 1.0, 0.0, 0.0}

{0.2222, 0.6235, 0.0556, 0.0432, 0.0556, 0.0, 0.0, 0.0, 0.0}

РЕШЕНИЕ

вероятность

Отнимем величину первого прыжка от всех результатов прыжков соперников, таким образом сведя задачу к “двойному” прыжку. Из условия задачи следует, что длина каждого прыжка является независимой случайной величиной, равномерно распределенной на отрезке [lower, upper]. Сумма двух прыжков также является случайной величиной, определенной на отрезке [2*lower, 2*upper]. Но она уже не будет равномерно распределенной.

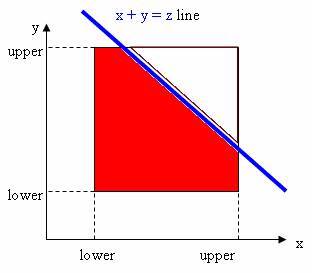
Определим случайную величину F(z) = {сумма двух прыжков не более z}. F(z) пропорционально площади области квадрата под прямой z = x + y, изображенной красным цветом.

Функция распределения F(z)имеет вид:

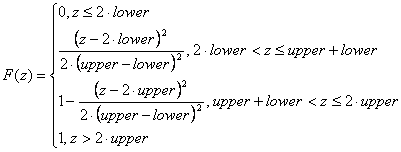
Отсортируем длины прыжков соперников по убыванию. Вероятность занять первое место равна 1 – F(opponents[0]). Вероятность занять второе место равна F(opponents[0]) – F(opponents[1]) и так далее. Вероятность занять последнее место равна F(opponents[n – 1]), где n – количество соперников.

ПРОГРАММА

#include <cstdio>

#include <vector>

#include <set>

#include <algorithm>

using namespace std;

double f(double lower, double upper, double z)

{

if (z <= 2 * lower) return 0.0;

if (z <= lower + upper) return (z – 2 * lower) * (z - 2*lower) / 2 /

(upper-lower) / (upper - lower);

if (z <= 2 * upper) return 1 - (z – 2 * upper) * (z – 2 * upper) / 2 /

(upper-lower) / (upper - lower);

return 1.0;

}

class TripleJump

{

public:

vector<double> getProbabilities(int lower, int upper, int first,

vector<int> opponents)

{

int i, n = (int)opponents.size();

vector<double> res(n + 1, 0);

for(i = 0; i < n; i++) opponents[i] -= first;

sort(opponents.begin(),opponents.end(),greater<int>());

res[0] = 1 - f(lower,upper,opponents[0]);

res[n] = f(lower,upper,opponents[n-1]);

for(i = 1; i < n; i++)

res[i] = f(lower,upper,opponents[i-1]) - f(lower,upper,opponents[i]);

return res;

}

};